UNIVERSAL LAW OF GRAVITATION
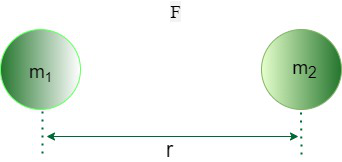
Every object in the universe attracts every other object with a force . Attraction force is directly proportional to the product of their masses.
F ∝ m1 × m2 Equation 1
The force between two objects is inversely proportional to the square of the distance between them, that is,
F ∝ 1/ r2 Equation 2
Combining Eqs. (1) and (2), we get
F ∝ m1 m2 / r2 Equation 3
F = G m1 m2 / r2 Equation 4
where G is the constant of proportionality and is called the universal gravitation constant.
m1 = Mass of one body
m2 = Mass of other body
r = Distance between two body
By multiplying crosswise, Eq. (4) gives
F × r 2 = G m1 × m2
G = F × r 2 / m1 × m2 Equation 5
The SI unit of G can be obtained by substituting the units of force, distance and mass in Eq. (5) as N m2 kg–2 = kg-1 m3 s-2
The C G S unit of G = Dyn cm2 g–2 = g-1 cm3 s-2
.
The value of G was found out by Henry Cavendish (1731 – 1810) by using a sensitive balance. The accepted value of G is 6.673 × 10–11 N m2 kg–2 , C G S value of G =6.673 × 10–8 dyn cm2 g–2
.

